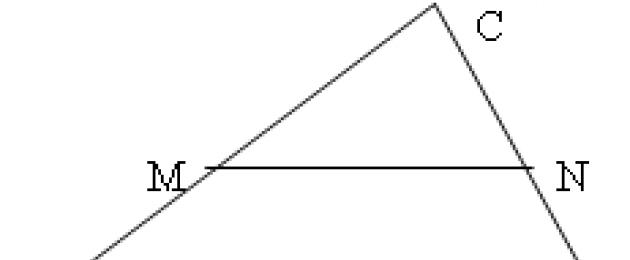
Вам интересно, как можно вычислить и найти среднюю линию треугольника. Тогда за дело.

Найти длину средней линии треугольника достаточно просто. Так как у треугольника три стороны, соответственно три угла и возможно может быть при построении три средних линий.

Что представляет собой треугольник:

Три стороны (равносторонний, равнобедренный)

Три угла (соответственно остроугольный, тупоугольный, прямоугольный треугольники)

Что такое средняя линия треугольника

Это отрезок. Отрезок соединяет середину двух сторон треугольника. У любого треугольника три средних линии.

Свойство 1: Средняя линия треугольника, параллельна стороне треугольника и равна его половине. Следовательно, для определения средней линии треугольника достаточно знать длину третьей стороны.

Пример: есть треугольник ABC, известно, что средняя сторона КN проведена параллельно АС. Длинна АС=8 см. AB=4 cм, ВС=4 см. Следовательно, для нахождения средней линии треугольника достаточно АС/2 и получить среднюю линию треугольника. Ответ: 4 см средняя линия в заданном треугольнике по существующим параметрам.

Свойство 2: Если в треугольнике провести три средних линий, то образуется четыре равных подобных треугольника. Коэффициент равен ½.

Свойство 3: Средняя линия равностороннего треугольника разбивает треугольник на трапецию и треугольник.

Пример решения задачи: Если мы нарисуем треугольник, то увидим, что вверху треугольника фигура с тремя углами. Внизу четырёхугольника фигура с двумя противоположными сторонами, которые параллельны друг другу.

Четырёхугольник, у которого только две стороны параллельны называются трапецией .

Параллельные стороны трапеции называются её основаниями , а те стороны, которые не параллельны, называются боковыми сторонами . Если боковые стороны равны, то такая трапеция является равнобедренной. Расстояние между основаниями называется высотой трапеции.

Средняя Линия Трапеции

Средняя линия - это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна её основаниям.

Теорема:

Если прямая, пересекающая середину одной боковой стороны, параллельна основаниям трапеции, то она делит пополам вторую боковую сторону трапеции.

Теорема:

Длина средней линии равна среднему арифметическому длин её оснований

MN средняя линия, AB и CD - основания, AD и BC - боковые стороны

MN = (AB + DC)/2

Теорема:

Длина средней линии трапеции равна среднему арифметическому длин её оснований.

Основная задача : Доказать, что средняя линия трапеции делит пополам отрезок, концы которого лежат в середине оснований трапеции.

Средняя Линия Треугольника

Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Она параллельна третьей стороне и её длина равна половине длины третьей стороны.
Теорема : Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне данного треугольника, то она делит третью сторону пополам.

AM = MC and BN = NC =>

Применение свойств средней линии треугольника и трапеции

Деление отрезка на определённое количество равных частей.
Задача: Разделить отрезок AB на 5 равных частей.
Решение:
Пусть p это случайный луч, у которого начало это точка А, и который не лежит на прямой AB. Мы последовательно откладываем 5 равных сегментов на p AA 1 = A 1 A 2 = A 2 A 3 = A 3 A 4 = A 4 A 5
Мы соединяем A 5 с B и проводим такие прямые через A 4 , A 3 , A 2 и A 1 , которые параллельны A 5 B. Они пересекают AB соответственно в точках B 4 , B 3 , B 2 и B 1 . Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции BB 3 A 3 A 5 мы видим, что BB 4 = B 4 B 3 . Таким же образом, из трапеции B 4 B 2 A 2 A 4 получаем B 4 B 3 = B 3 B 2

В то время как из трапеции B 3 B 1 A 1 A 3 , B 3 B 2 = B 2 B 1 .
Тогда из B 2 AA 2 следует, что B 2 B 1 = B 1 A. В заключении получаем:
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
Ясно, что для разделения отрезка AB на другое количество равных частей, нам нужно проецировать то же самое количество равных сегментов на луч p. И далее продолжать вышеописанным способом.

Средняя линия трапеции, а особенно ее свойства, очень часто используются в геометрии для решения задач и доказательства тех или иных теорем.

– это четырехугольник, у которого только 2 стороны параллельны друг другу. Параллельные стороны называют основаниями (на рисунке 1 - AD и BC ), две другие – боковыми (на рисунке AB и CD ).

Средняя линия трапеции – это отрезок, соединяющий середины ее боковых сторон (на рисунке 1 - KL ).

Свойства средней линии трапеции

Доказательство теоремы о средней линии трапеции

Доказать , что средняя линия трапеции равна полусумме ее оснований и параллельна этим основаниям.

Дана трапеция ABCD со средней линией KL . Для доказательства рассматриваемых свойств требуется провести прямую через точки B и L . На рисунке 2 это прямая BQ . А также продолжить основание AD до пересечения с прямой BQ .

Рассмотрим полученные треугольники LBC и LQD :

1. По определению средней линии KL точка L является серединой отрезка CD . Отсюда следует, что отрезки CL и LD равны.
2. ∠ BLC = ∠ QLD , так как эти углы вертикальные.
3. ∠ BCL = ∠ LDQ , так как эти углы накрест лежащие при параллельных прямых AD и BC и секущей CD .

Из этих 3 равенств следует, что рассмотренные ранее треугольники LBC и LQD равны по 1 стороне и двум прилежащим к ней углам (см. рис. 3). Следовательно, ∠ LBC = ∠ LQD , BC=DQ и самое главное - BL=LQ => KL , являющаяся средней линией трапеции ABCD , также является и средней линией треугольника ABQ . Согласно свойству средней линией треугольника ABQ получаем.

Средняя линия треугольника – это отрезок, соединяющий середины 2-х его сторон. Соответственно, каждого у треугольника три средних линии. Зная качество средней линии, а также длины сторон треугольника и его углы, дозволено обнаружить длину средней линии.

Вам понадобится

• Стороны треугольника, углы треугольника

Инструкция

1. Пускай в треугольнике ABC MN – средняя линия, соединяющая середины сторон AB (точка M) и AC (точка N).По свойству средняя линия треугольника, соединяющая середины 2-х сторон, параллельна третьей стороне и равна её половине. Значит, средняя линия MN будет параллельна стороне BC и равна BC/2.Следственно, для определения длины средней линии треугольника довольно знать длину стороны именно этой третьей стороны.

2. Пускай сейчас вестимы стороны, середины которых соединяет средняя линия MN, то есть AB и AC, а также угол BAC между ними. Потому что MN – средняя линия, то AM = AB/2, а AN = AC/2.Тогда по теореме косинусов объективно: MN^2 = (AM^2)+(AN^2)-2*AM*AN*cos(BAC) = (AB^2/4)+(AC^2/4)-AB*AC*cos(BAC)/2. Отсель, MN = sqrt((AB^2/4)+(AC^2/4)-AB*AC*cos(BAC)/2).

3. Если знамениты стороны AB и AC, то среднюю линию MN дозволено обнаружить, зная угол ABC либо ACB. Пускай, скажем, знаменит угол ABC. Потому что по свойству средней линии MN параллельна BC, то углы ABC и AMN – соответствующие, и, следственно, ABC = AMN. Тогда по теореме косинусов: AN^2 = AC^2/4 = (AM^2)+(MN^2)-2*AM*MN*cos(AMN). Следственно, сторону MN дозволено обнаружить из квадратного уравнения (MN^2)-AB*MN*cos(ABC)-(AC^2/4) = 0.

Совет 2: Как обнаружить сторону квадратного треугольника

Квадратный треугольник больше верно именуется прямоугольным треугольником. Соотношения между сторонами и углами этой геометрической фигуры детально рассматриваются в математической дисциплине тригонометрии.

Вам понадобится

• – лист бумаги;
• – ручка;
• – таблицы Брадиса;
• – калькулятор.

Инструкция

1. Обнаружьте сторону прямоугольного треугольника с поддержкой теоремы Пифагора. Согласно этой теореме, квадрат гипотенузы равен сумме квадратов катетов: с2 = a2+b2 , где с – гипотенуза треугольника , a и b – его катеты. Дабы применить это уравнение, надобно знать длину всяких 2-х сторон прямоугольного треугольника .

2. Если по условиям заданы размеры катетов, разыщите длину гипотенузы. Для этого с поддержкой калькулятора извлеките квадратный корень из суммы катетов, всякий из которых заранее возведите в квадрат.

3. Вычислите длину одного из катетов, если вестимы размеры гипотенузы и иного катета. При помощи калькулятора извлеките квадратный корень из разности гипотенузы в квадрате и вестимого катета, также возведенного в квадрат.

4. Если в задаче заданы гипотенуза и один из прилежащих к ней острых углов, используйте таблицы Брадиса. В них приведены значения тригонометрических функций для большого числа углов. Воспользуйтесь калькулятором с функциями синуса и косинуса, а также теоремами тригонометрии, которые описывают соотношения между сторонами и углами прямоугольного треугольника .

5. Обнаружьте катеты при помощи основных тригонометрических функций: a = c*sin ?, b = c*cos ?, где а – катет, противолежащий к углу?, b – катет, прилежащий к углу?. Сходственным образом посчитайте размер сторон треугольника , если заданы гипотенуза и иной острый угол: b = c*sin ?, a = c*cos ?, где b – катет, противолежащий к углу?, а – катет, прилежащий к углу?.

6. В случае, когда вестим катет a и прилежащий к нему острый угол?, не забывайте, что в прямоугольном треугольнике сумма острых углов неизменно равна 90°: ? + ? = 90°. Разыщите значение угла, противолежащего к катету а: ? = 90° – ?. Либо воспользуйтесь тригонометрическими формулами приведения: sin ? = sin (90° – ?) = cos ?; tg ? = tg (90° – ?) = ctg ? = 1/tg ?.

7. Если вестим катет а и противолежащий к нему острый угол?, при помощи таблиц Брадиса, калькулятора и тригонометрических функций вычислите гипотенузу по формуле: c=a*sin ?, катет: b=a*tg ?.

Видео по теме