Уравнением времени называется разность между среднем временем и истинным солнечным временем в один и тот же момент времени.
ȵ = T m - = t m - = - α m
Следовательно: T m = + ȵ. Но = + 12 r ; - измеряется.
= + 12 r + ȵ.

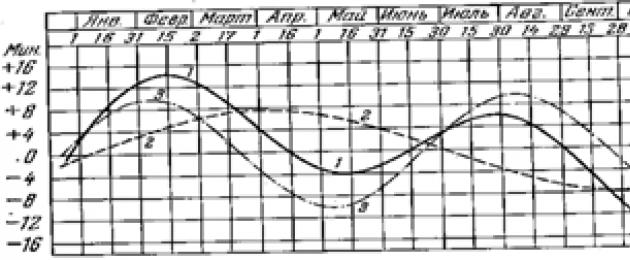
Рис 15. График уравнения времени: 1 – уравнение времени, 2 – уравнение центра, 3 - уравнение от наклона эклиптики
Кривая уравнения времени является суммой двух синусоид.
Синусоида с годичным периодом дает разность между истинным и средним временем, обусловленную неравномерным движением Солнца по эклиптике. Эта часть уравнения времени – уравнение центра или уравнение от эксцентриситета.
Уравнение от наклона эклиптики – синусоида с полугодичным периодом.
Уравнение времени публикуется в астрономических календарях и ежегодниках.
Примечание: Тропический год содержит 365,2422 средних солнечных суток, 365,2422 звездных суток.
За одни звездные сутки точка 𝛶 весеннего равноденствия возвращается на небесный меридиан. Среднее экваториальное Солнце не дойдет до него, так как оно сместится по небесному экватору на 1 0 , что приведет к запаздыванию около 4 минут, точнее 3 мин. 56 сек. Настолько средние солнечные сутки продолжительнее звездных.
Системы счета времени
Среднее гринвичское (всемирное) время – среднее время на географическом меридиане Гринвича – Т 0 .
Его также называют мировым или универсальным, обозначают u Т.
На географической широте λ
Т λ = Т 0 + λ. Т λ = Т m
λ>0 к востоку от Гринвича.
Время Т λ измеренное на данном географическом меридиане –местное время. Это время неудобно!!!
1884 г. принята поясная система счета времени. Счетчик времени ведется только на 24 основных географических меридианах, расположенных приблизительно посередине каждого часового пояса.
Границы часовых поясов точно следуют по географическим меридианам только в открытых морях и океанах. Номера поясов от 0 до 23. За основной меридиан нулевого пояса принят меридиан Гринвича.
Поясное время – Т n – местное среднее солнечное время основного меридиана данного пояса. T m – T n = λ – n h . λ – восточная долгота от Гринвича; n h – число целых часов, равное номеру пояса. T n = Т 0 + n h ; Т 0 – всемирное время.
Декретное время – вводится специальными постановлениями в целях экономии электроэнергии.
Ньютоновское или эфемеридное время – равномерное время, которое является аргументом при вычислении эфемерид планет и определяется по движению Луны и планеты.
Средние солнечные сутки оказываются непостоянной величиной вследствие неравномерного вращения Земли, вследствие тормозящих действий лунных приливов и отливов, (вековые изменения), сезонных перераспределений воздушных и воздушных и водных масс на поверхности Земли.
В астрономических ежегодниках эфемериды Солнца, Луны, планет и спутников даются в системе эфемеридного времени. Для вычисления положения этих небесных тел в системе всемирного (неравномерного) времени вводится поправкаТ, которая определяется для прошедших моментов времени.
В 1900 г.Т = 0. За 75 лет скорость вращения Земли в среднем уменьшалась и
Вообще любое уравнение - это математическая модель чашечных весов (рычажных, равноплечих, коромысловых - названий много), изобретенных в древнем Вавилоне 7000 лет назад или еще раньше. Более того, я даже думаю, что именно чашечные весы, использовавшиеся на древнейших базарах, и стали прообразом уравнений. И если смотреть на любое уравнение не как на непонятный набор цифр и букв, связанный двумя параллельными палочками, а как на чаши весов, то и со всем остальным проблем не будет:
Любое уравнение подобно уравновешенным чашам весов
Так уж получилось, что уравнений в нашей жизни с каждым днем все больше, а понимания, что такое уравнение и в чем его смысл - все меньше. Во всяком случае у меня сложилось такое впечатление при попытке объяснить старшей дочери смысл простейшего математического уравнения типа:
х + 2 = 8 (500.1)
Т.е. в школе конечно же объясняют, что в таких случаях чтобы найти х , нужно из правой части вычесть 2:
х = 8 - 2 (500.3)
Это, конечно же, абсолютно правильное действие, но почему нужно именно вычесть, а не, например, прибавить или разделить, в школьных учебниках объяснения нет. Просто есть правило, которое нужно тупо выучить:
При переносе члена уравнения из одной части в другую его знак меняется на противоположный .
А как сие правило понимать школьнику 10 лет от роду и в чем его смысл, это вы уж сами думайте-решайте. Более того, выяснилось, что и мои близкие родственники тоже никогда не понимали смысла уравнений, а просто заучивали на память то, что требовалось (и вышеуказанное правило в частности), а уж потом применяли это, как бог на душу положит. Мне такое положение дел не понравилось, поэтому я и решил написать данную статью (растет младший, ему через несколько лет опять придется это объяснять, да и немногочисленным читателям моего сайта это тоже может пригодиться).
Сразу хочу сказать, что хоть я 10 лет учился в школе, но при этом никаких правил и определений, относящихся к техническим дисциплинам, никогда не учил. Т.е. если что-то понятно, то оно и так запомнится, а если что-то не понятно, то какой смысл его зубрить, не понимая смысла, если оно все равно забудется? А кроме того, если мне что-то не понятно, значит, оно мне и не надо (это я только недавно осознал, что если я чего-то не понимал в школе, то это была не моя вина, а вина преподавателей, учебников и вообще системы образования).
Такой подход обеспечивал мне массу свободного времени, которого в детстве так не хватает на всякие игры и развлечения. При этом я участвовал в различных олимпиадах по физике, химии, а одну районную по математике даже выиграл. Но время шло, количество дисциплин, оперирующих абстрактными понятиями, только увеличивалось и соответственно мои оценки снижались. На первом курсе института количество дисциплин, оперирующих абстрактными понятиями, составляло абсолютное большинство и я конечно же был полным троечником. Но потом, когда мне по ряду причин пришлось самому без помощи лекций и конспектов разбираться с сопроматом и я его как бы понял, дело пошло на лад и закончилось красным дипломом. Впрочем сейчас не об этом, а о том, что в связи с указанной спецификой мои понятия и определения могут значительно отличаться от преподаваемых в школе.
А теперь продолжим
Простейшие уравнения, аналогия с весами
Вообще-то детей приучают сравнивать различные предметы еще в дошкольном возрасте, когда они еще и говорить-то толком не умеют. Начинают как правило с геометрических сравнений. Например, показывают ребенку два кубика и ребенок должен определить, какой кубик больше, а какой меньше. А если они одинаковые, то это и есть равенство по размеру. Затем задача усложняется, ребенку показывают предметы различных форм, различных цветов и выбрать одинаковые предметы ребенку становится все сложнее. Однако мы не будем так сильно усложнять задачу, а остановимся лишь на одном виде равенства - денежно-весовом.
Когда чаши весов находятся на одном горизонтальном уровне (стрелки чашечных весов, показанные на рисунке 500.1 оранжевым и голубым цветом, совпадают, горизонтальный уровень показан черной жирной чертой), то это значит, что на правой чаше весов находится столько же груза, сколько на левой чаше. В простейшем случае это могут быть гири весом в 1 кг:
Рисунок 500.1.
И тогда мы получаем простейшее уравнение 1 = 1. Впрочем уравнение это только для меня, в математике подобные выражения называют равенством, но суть от этого не меняется. Если мы с левой чаши весов уберем гирю и положим на нее что угодно, хоть яблоки, хоть гвозди, хоть красную икру и при этом чаши весов будут на одном горизонтальном уровне, то это будет по-прежнему означать, что 1 кг любого из указанных продуктов равен 1 кг гирьки, оставшейся на правой части весов. Остается лишь заплатить за этот килограмм согласно установленной продавцом цене. Другое дело, что вам может не нравиться цена, или возникли сомнения в точности весов - но это уже вопросы экономико-правовых отношений, к математике прямого отношения не имеющие.
Конечно же, в те далекие времена, когда появились чашечные весы, все было значительно проще. Во-первых, не было такой меры веса, как килограмм, а были денежные единицы, соответствующие мерам весов, например, таланты, шекели, фунты, гривны и пр. (кстати, меня давно удивляло, что есть фунт - денежная единица и фунт - мера веса, есть гривна - денежная единица, а когда-то гривна была мерой веса, и только недавно, когда я узнал, что талант - это не только денежная единица древних иудеев, упоминаемая в Ветхом завете, но и мера веса, принятая в древнем Вавилоне, все встало на свои места).
Точнее сначала были меры весов, как правило зерна злаковых культур, а уже потом появились деньги, этим мерам весов соответствующие. Например 60 зерен соответствовали одному шекелю (сиклю), 60 шекелей - одной мине, а 60 мин - одному таланту. Поэтому изначально весы использовались для того, чтобы проверить, не являются ли предлагаемые деньги фальшивыми, а уже потом появились гирьки, как эквивалент денег, обвесы и обсчеты, электронные весы и пластиковые карты, но сути дела это никак не меняет.
В те далекие времена продавцу не нужно было долго и подробно объяснять, сколько будет стоить тот или иной товар. Достаточно было положить на одну чашу весов продаваемый товар, а на вторую покупатель клал деньги - очень просто и наглядно и даже знание местного наречия не требуется, можно торговать в любой точке мира. Но вернемся к уравнениям.
Если рассматривать уравнение (500.1) с позиции весов, то оно означает, что на левой чаше весов находится неизвестное количество килограммов и еще 2 килограмма, а на правой чаше - 8 килограммов:
х + 2кг , = 8кг , (500.1.2)
Примечание : В данном случае нижнее подчеркивание символизирует дно чаш весов, при расчетах на бумаге эта линия может больше напоминать дно чаши весов. Более того, математики уже давно придумали специальные символы - скобки, так вот любые скобки можно рассматривать как борта чаш весов, во всяком случае на первом этапе постижения смысла уравнений. Тем не менее нижнее подчеркивание я для большей наглядности оставлю.
Итак, что нам нужно сделать, что узнать неизвестное количество килограммов? Правильно! Снять с левой и с правой части весов по 2 килограмма, тогда чаши весов останутся на одном горизонтальном уровне, т.е.у нас будет по прежнему равенство:
х + 2кг , - 2кг = 8кг , - 2кг (500.2.2)
Соответственно
х , = 8кг - 2кг , (500.3.2)
х , = 6 кг , (500.4.2)

Рисунок 500.2.
Часто математика оперирует не килограммами, а некими абстрактными безразмерными единицами и тогда запись решения уравнения (500.1) например в черновике будет выглядеть так:
х + 2 , = 8 , (500.1)
х + 2 , - 2 = 8 , - 2 (500.2)
х , = 8 - 2 , (500.3)
х = 6 (500.4)
Что и отражено на рисунке 500.2.
Примечание : Формально для еще более лучшего понимания после уравнения (500.2) должно следовать еще одно уравнение вида: х + 2 - 2 , = 8 - 2 , означающее, что действие завершилось и мы опять имеем дело с равновесными чашами весом. Однако на мой взгляд в такой совсем уж полной записи решения необходимости нет.
В чистовиках обычно используется сокращенная запись решения уравнения, причем сокращаются не только столь необходимые на мой взгляд на начальном этапе изучения уравнений символы чаш весов, но даже и целые уравнения. Так сокращенная запись решения уравнения (500.1) в чистовике согласно приводимым в учебниках примерам будет выглядеть так:
х + 2 = 8 (500.1.1)
х = 8 - 2 (500.3.1)
х = 6 (500.4)
В итоге, при использовании аналогии с весами мы составили дополнительное уравнение (500.2) по сравнению с предлагаемым учебниками то ли методом решения, то ли формой записи этого решения. На мой взгляд это уравнение, к тому же записанное приблизительно в такой форме, т.е. с символичным обозначением чаш весов - это и есть то недостающее звено, важное для понимания смысла уравнений.
Т.е. при решении уравнений мы ничего и никуда с обратным знаком не переносим, а выполняем одинаковые математические действия с левой и с правой частью уравнения.
Просто сейчас принято записывать решение уравнений в сокращенной форме, приведенной выше. За уравнением (500.1.1) сразу следует уравнение (500.3.1), отсюда и следует правило обратных знаков, которое впрочем многим проще запомнить, чем вникать в смысл уравнений.
Примечание : Против сокращенной формы записи я ничего не имею, более того. продвинутые пользователи могут эту форму еще более сокращать, однако делать это следует лишь после того, когда общий смысл уравнений уже четко усвоен.
А еще расширенная запись позволяет понять главные правила решения уравнений:
1. Если мы производим одинаковые математические действия с левой и правой частью уравнений, то равенство сохраняется .
2. Не важно, какая часть в рассматриваемом уравнении левая, а какая правая, мы можем свободно менять их местами .
Эти математические действия могут быть любыми. Мы можем вычитать одно и то же число из левой и из правой части, как показано выше. Мы можем прибавлять одно и то же число к левой и правой части уравнения, например:
х - 2 , = 8 , (500.5.1)
х - 2 , + 2 = 8 , + 2 (500.5.2)
х , = 8 + 2 , (500.5.3)
х = 10 (500.5.4)
Мы можем делить или умножать обе части на одно и то же число, например:
3х , = 12 , (500.6.1)
3х , : 3 = 12 , : 3 (500.6.2)
х , = 12 : 3 , (500.6.3)
х = 4 (500.6.4)
3х - 6 , = 12 , (500.7.1)
3х - 6 , + 6 = 12 , + 6 (500.7.2)
3х , = 18 , (500.7.3)
3х , : 3 = 18 , : 3 (500.7.4)
х = 6 (500.7.5)
Мы можем интегрировать или дифференцировать обе части. Мы можем делать все, что угодно с левой и правой частью, но если эти действия будут одинаковыми для левой и правой части, то равенство сохранится (чаши весов останутся на одном горизонтальном уровне).
Конечно же действия нужно выбирать такие, которые позволят максимально быстро и просто определить неизвестную величину.
С этой точки зрения классический метод обратного действия как бы более прост, но как быть, если ребенок еще не изучал отрицательные числа? А между тем составленное уравнение имеет следующий вид:
5 - х = 3 (500.8)
Т.е. при решении этого уравнения классическим методом один из возможных вариантов решения, дающий самую короткую запись, следующий:
- х = 3 - 5 (500.8.2)
- х = - 2 (500.8.3)
х = 2 (500.8.4)
И самое главное - как тут объяснить ребенку почему уравнение (500.8.3) тождественно уравнению (500.8.4)?
Это значит, что в данном случае даже при использовании классического метода экономить на записи нет никакого смысла и сначала нужно избавиться от неизвестной величины в левой части, имеющей отрицательный знак.
5 - х = 3 (500.8)
5 = 3 + х (500.8.5)
3 + х = 5 (500.8.6)
х = 5 - 3 (500.8.7)
х = 2 (500.8.4)
При этом полная запись будет выглядеть так:
5 - х , = 3 , (500.8)
5 - х , + х = 3 , + х (500.9.2)
5 , = 3 + х , (500.9.3)
3 + х , = 5 , (500.8.6)
3 + х , - 3 = 5 , - 3 (500.9.3)
х , = 5 - 3 , (500.8.7)
х = 2 (500.8.4)
Добавлю еще раз. Полная запись решения нужна не для учителей, а для лучшего понимания метода решения уравнений. А когда мы меняем местами левую и правую части уравнения, то это все равно что мы меняем взгляд на весы с точки зрения покупателя на точку зрения продавца, тем не менее равенство при этом сохраняется.
К сожалению, я так и не смог добиться от своей дочери полной записи решения даже в черновиках. У нее железный довод: "нас так не учили". А между тем сложность составляемых уравнений увеличивается, процент угадываний, какое действие нужно выполнить для определения неизвестной величины, уменьшается, оценки падают. Что с этим делать, не знаю...
Примечание : в современной математике принято различать равенства и уравнения, т.е. 1 = 1 - это просто численное равенство, а если в одной из частей равенства есть неизвестная, которую необходимо найти, то это уже уравнение. Как по мне, то такое дифференцирование значений не имеет большого смысла, а лишь усложняет восприятие материала. Я считаю, что любое равенство можно называть уравнением, а любое уравнение основано на равенстве. А кроме того, возникает вопрос х = 6, это уже равенство или это еще уравнение?
Простейшие уравнения, аналогия со временем
Конечно же, аналогия с весами при решении уравнений является далеко не единственной. Например, решение уравнений можно рассматривать и во временном аспекте. Тогда условие, описываемое уравнением (500.1), будет звучать так:
После того, как мы добавили к неизвестному количеству х еще 2 единицы, у нас стало 8 единиц (настоящее время). Однако нас по тем или иным причинам не интересует, сколько их стало, а интересует сколько их было в прошедшем времени. Соответственно, чтобы узнать, сколько у нас было этих самых единиц, нам нужно произвести обратное действие, т.е. от 8 отнять 2 (уравнение 500.3). Такой подход точно соответствует излагаемому в учебниках, но на мой взгляд, является не таким наглядным, как аналогия с весами. Впрочем мнения по этому поводу могут быть разные.
Пример решения уравнения со скобками
Эту статью я написал летом, когда дочь окончила 4 класс, но не прошло и полгода, как им в школе начали задавать решение уравнений следующего вида:
(97 + 75: (50 - 5х)) · 3 = 300 (500.10)
Никто в классе решить это уравнение не смог, а между тем в его решении при применении предложенного мной способа нет ничего сложного, вот только полная форма записи будет занимать слишком много места:
(500.10.2)
97 + 75: (50 - 5х) , = 300: 3 , (500.10.3)
97 + 75: (50 - 5х) , = 100 , (500.10.4)
(500.10.5)
75: (50 - 5х) , = 100 - 97 , (500.10.6)
75: (50 - 5х) , = 3 , (500.10.7)
(500.10.8)
75 , = 3 · (50 - 5х) , (500.10.9)
(500.10.10)
75: 3 , = 50 - 5х , (500.10.11)
25 , = 50 - 5х , (500.10.12)
25 , + 5х = 50 - 5х , + 5х (500.10.13)
25 + 5х , = 50 , (500.10.14)
25 + 5х , - 25 = 50 , - 25 (500.10.15)
5х , = 50 - 25 , (500.10.16)
5х , = 25 , (500.10.17)
5х , : 5 = 25 , : 5 (500.10.18)
х , = 25: 5 , (500.10.19)
х = 5 (500.10.20)
Однако на данном этапе в такой полной форме записи нет никакой необходимости. Раз уж мы добрались до двойных скобок, то не обязательно для математических операций в левой и правой части составлять отдельное уравнение, поэтому запись решения в черновике вполне может выглядеть так:
97 + 75: (50 - 5х) , : 3 = 300 , : 3, (500.10.2)
97 + 75: (50 - 5х) , = 100 , (500.10.4)
97 + 75: (50 - 5х) , - 97 = 100 - 97 , (500.10.5)
75: (50 - 5х) , = 3 , (500.10.7)
75: (50 - 5х) , · (50 - 5х) = 3 , · (50 - 5х) (500.10.8)
75 , = 3 · (50 - 5х) , (500.10.9)
75 , : 3 = 3 · (50 - 5х) , : 3 (500.10.10)
25 , = 50 - 5х , (500.10.12)
25 , + 5х = 50 - 5х , + 5х (500.10.13)
25 + 5х , = 50 , (500.10.14)
25 + 5х , - 25 = 50 , - 25 (500.10.15)
5х , = 25 , (500.10.17)
5х , : 5 = 25 , : 5 (500.10.18)
х = 5 (500.10.20)
Итого на данном этапе потребовалось записать 14 уравнений для решения исходного.
При этом запись решения уравнения в чистовике может выглядеть так:
97 + 75: (50 - 5х) = 300: 3 (500.10.3)
97 + 75: (50 - 5х) = 100 (500.10.4)
75: (50 - 5х) = 100 - 97 (500.10.6)
75: (50 - 5х) = 3 (500.10.7)
75 = 3 · (50 - 5х) (500.10.9)
75: 3 = 50 - 5х (500.10.11)
25 = 50 - 5х (500.10.12)
25 + 5х = 50 (500.10.14)
5х = 50 - 25 (500.10.16)
5х = 25 500.10.17)
х = 25: 5 (500.10.19)
х = 5 (500.10.20)
Т.е. при сокращенной форме записи нам все равно придется составить 12 уравнений. Экономия в записи при этом минимальная, а вот с пониманием требуемых действий у пятиклассника действительно могут возникнуть проблемы.
P.S. Только когда дело дошло до двойных скобок, дочь заинтересовалась предложенным мной методом решения уравнений, но при этом в ее форме записи даже в черновике все равно уравнений в 2 раза меньше, потому что она пропускает итоговые уравнения типа (500.10.4), (500.10.7) и им подобные, а при записи сразу оставляет место для следующего математического действия. В итоге запись в ее черновике выглядела примерно так:
(97 + 75: (50 - 5х)) · 3 , : 3 = 300 , : 3 (500.10.2)
97 + 75: (50 - 5х) , - 97 = 100 , - 97 (500.10.5)
75: (50 - 5х) , · (50 - 5х) = 3 , · (50 - 5х) (500.10.8)
75 , : 3 = 3 · (50 - 5х) , : 3 (500.10.10)
25 , + 5х = 50 - 5х , + 5х (500.10.13)
25 + 5х , - 25 = 50 , - 25 (500.10.15)
5х , : 5 = 25 , : 5 (500.10.18)
х = 5 (500.10.20)
В итоге получилось всего 8 уравнений, что даже меньше, чем требуется при сокращенной записи решения. В принципе я не возражаю, вот только была бы от этого польза.
Вот собственно и все, что мне хотелось сказать по поводу решения простейших уравнений, содержащих одну неизвестную величину. Для решения уравнений, содержащих две неизвестных величины, потребуется
Системы истинного и среднего солнечного времени.
Система звездного времени
Звездное время обозначается s. Параметрами системы звездного времени являются:
1) механизм – вращение Земли вокруг своей оси;
2) масштаб - звездные сутки, равные промежутку времени между двумя последовательными верхними кульминациями точки весеннего равноденствия в пункте наблюдения;
3) начальная точка на небесной сфере - точка весеннегоравноденствия g, нульпункт (начало звездных суток) - момент верхней кульминации точки g;
4) способ отсчета. Мера измерения звездного времени - часовой угол точки весеннего равноденствия, t g . Измерить его невозможно, но для любой звезды справедливо выражение
s = t g = a + t,
следовательно, зная прямое восхождение звезды a и вычисляя ее часовой угол t, можно определить звездное время s.
Система звездного времени применяется при определении географических координат пунктов на поверхности Земли и азимутов направления на земные предметы, при изучении неравномерностей суточного вращения Земли, при установлении нульпунктов шкал других систем измерения времени. Эта система, хоть и широко применяется в астрономии, в повседневной жизни неудобна. Смена дня и ночи, обусловленная видимым суточным движением Солнца, создает вполне определенный цикл в деятельности человека на Земле. Поэтому издавна счисление времени ведется по суточному движению Солнца.
Система истинного солнечного времени (или истинное солнечное время - m ¤) применяется при астрономических или геодезических наблюдениях Солнца. Параметры системы:
1) механизм - вращение Земли вокруг своей оси;
2) масштаб - истинные солнечные сутки - промежуток времени между двумя последовательными нижними кульминациями центра истинного Солнца;
3) начальная точка - центр диска истинного Солнца - ¤, нульпункт - истинная полночь, или момент нижней кульминации центра диска истинного Солнца;
4) cпособ отсчета. Мера измерения истинного солнечного времени - геоцентрический часовой угол истинного Солнца t ¤ плюс 12 часов:
m ¤ = t ¤ + 12 h .
Единица истинного солнечного времени - секунда, равная 1/86400 истинных солнечных суток, не удовлетворяет основному требованию, предъявляемому к единице измерения времени - она не постоянна.
Причинами непостоянства шкалы истинного солнечного времени являются:
1) неравномерное движение Солнца по эклиптике вследствие эллиптичности орбиты Земли;
2) неравномерное возрастание прямого восхождения Солнца в течение года, так как Солнце по эклиптике, наклоненной к небесному экватору под углом примерно 23.5 0 .
Вследствие этих причин применение системы истинного солнечного времени на практике неудобно. Переход к равномерной шкале солнечного времени происходит в два этапа.
Этап 1 - переход к фиктивному среднему эклиптическому Солнцу. На данном этапе исключается неравномерность движения Солнца по эклиптике. Неравномерное движение по эллиптической орбите заменяется равномерным движением по круговой орбите. Истинное Солнце и среднее эклиптическое Солнце совпадают, когда Земля проходит через перигелий и афелий своей орбиты.
Этап 2 - переход к среднему экваториальному Солнцу. Здесь исключается неравномерность возрастания прямого восхождения Солнца, обусловленная наклоном эклиптики. Истинное Солнце и среднее экваториальное Солнце одновременно проходят точки весеннего и осеннего равноденствия.
В результате перечисленных действий вводится новая система измерения времени – среднее солнечное время .
Среднее солнечное время обозначается m. Параметрами системы среднего солнечного времени являются:
1) механизм - вращение Земли вокруг оси;
2) масштаб - средние сутки - промежуток времени между двумя последовательными нижними кульминациями среднего экваториального Солнца ¤ экв;
3) начальная точка - среднее экваториальное Солнце ¤ экв, нульпункт - средняя полночь, или момент нижней кульминации среднего экваториального Солнца;
4) способ отсчета. Мерой измерения среднего времени является геоцентрический часовой угол среднего экваториального Солнца t ¤ экв плюс 12 часов.
m = t ¤ экв + 12 h .
Определить среднее солнечное время непосредственно из наблюдений нельзя, так как среднее экваториальное Солнце – фиктивная точка на небесной сфере. Среднее солнечное время вычисляют по истинному солнечному времени, определенному из наблюдений истинного Солнца. Разность истинного солнечного времени m ¤ и среднего солнечного времени m называется уравнением времени и обозначается h:
h = m ¤ - m = t ¤ - t ¤ ср.экв. .
Уравнение времени выражается двумя синусоидами с годовым и полугодовым периодами:
h = h 1 + h 2 » -7.7 m sin (l + 79 0)+ 9.5 m sin 2l,
где l – эклиптическая долгота среднего эклиптического Солнца.
График h есть кривая с двумя максимумами и двумя минимумами, которая в декартовой прямоугольной системе координат имеет вид, показанный на рисю17.
Мы ведем счет времени, используя "среднее солнце" - воображаемую точку, которая в течение года равномерно движется по небесному экватору. Но ведь настоящее Солнце движется по эклиптике, причем неравномерно.
Уравнением времени называется разность между средним и истинным солнечным временем или разности прямых восхождений истинного и среднего Солнца. Эта разница возникает по двум причинам:
1) Земля имеет эллиптическую орбиту и движется по ней неравномерно, с максимальной скоростью в перигелии (около 2 января) и с минимальной в афелии (около 6 июля)
2) Из-за наклона эклиптики к экватору вблизи равноденствий проекция скорости Солнца на экватор меньше, чем в период солнцестояний, когда оно движется параллельно экватору.
Эти отклонения складываются, образуя довольно сложную кривую (темно-красная линия на графике).
Однако на самом деле этот график довольно прост для построения.
Поправка, вызванная эллиптичностью земной орбиты, имеет период, равный периоду обращения Земли, т.е. одному году, наиболее быстро эта ошибка нарастает, когда Земля находится в перигелии, ближе всего к Солнцу и движется по орбите с максимальной скоростью. График этой ошибки представляет собой синусоиду с начальной точкой в дате перигелия (голубая кривая).
Поправка, вызванная наклоном эклиптики, имеет период в полгода, так как за год Солнце дважды проходит точки равноденствий и дважды - солнцестояний. Ее график - тоже синусоида, только нулевая точка ее соответствует максимальной скорости движения проекции Солнца на экватор - дню солнцестояния (желтая кривая).
Амплитуды этих составляющих близки и составляют 7.8 градусов для первой, и 10 градусов - для второй. Теперь мы можем легко построить графики обеих составляющих уравнения времени и определить их суммарное значение. Это можно сделать даже графически, определяя значение поправки по проекции точки на окружности с соответствующим радиусом. Только горизонтальной оси будут соответствовать различные даты - 22 декабря и 2 января соответственно. (Пример аналогичного построения смотрите в работе по определению географических координат - там этим способом находилось склонение Солнца).
Исходя из этих рассуждений легко построить и математическое выражение для определения уравнения времени:
η=7.8*sin(D-2)+10*sin(2D+10) , где
D=(d*360/365) - приращение долготы среднего Солнца от начала года;
d - порядковый номер дня в году.
Эта формула эмпирическая, приближенная, однако обеспечивает точность не хуже 1/2 минуты, а самое главное - для ее вывода нужно только понимание причин возникновения расхождений в среднем и истинном солнечном времени и два коэффициента, характеризующих величину каждой поправки.
Математическая сторона основной задачи строительной механики основана на зависимостях, полученных в сопромате. Напомним их на примере напряженно-деформированного состояния элемента рамы, для которого – в отличие от балки – поперечный изгиб сопровождается дополнительным растяжением или сжатием.
Пусть такой элемент длиной dx расположен в локальной системе координат Oxy , где ось Ox направлена по оси стержня, и загружен распределенной нагрузкой интенсивностью q x и q y вдоль Ox и Oy соответственно (рис. 1.20).
Напряженно-деформированное состояние стержня определяется девятью компонентами:
– внутренними усилиями (M , Q , N ,);
– перемещениями (u , v , );
– деформациями (κ, , ).
Уравнения для определения этих функций можно разделить на три группы:
Статические уравнения – связывают внутренние усилия (рис. 1.20, б) с заданной нагрузкой:
dN /dx = – q x ;
dQ /dx = q y ; ý (1.10)
dM /dx = Q .
Геометрические уравнения – выражают деформации через перемещения, показанные на рис. 1.20, б, в:
κ = d /dx ;
= dv /dx ; (1.11)
= du /dx .
Физические уравнения – представляют собой зависимости между внутренними усилиями и деформациями:
κ = M /EJ ;
= Q /GF ; (1.12)
= N /EF ;
где E – модуль Юнга;
G – модуль сдвига;
F – площадь поперечного сечения стержня;
J – момент его инерции;
– коэффициент, учитывающий неравномерность распределения касательных напряжений в поперечном сечении стержня.
Отметим, что выражения EJ и EF в (1.12) называются жесткостями стержня при изгибе и растяжении (сжатии) соответственно.
При решении системы уравнений (1.10) – (1.12) возможны два варианта:
1) внутренние усилия M , Q , N , удается найти из системы уравнений (1.10), не обращаясь к остальным уравнениям – это СОС;
2) внутренние усилия можно найти только путем совместного решения всех девяти уравнений – это СНС.
В последнем случае при решении этих уравнений возможны два подхода:
– в качестве основных неизвестных выбирают усилия M , Q , N , выражая все остальные через них – это решение в форме метода сил ;
– в качестве основных неизвестных выбирают перемещения u , v , – это решение в форме метода перемещений .
Системы, описываемые линейными уравнениями (1.10) (1.12), называются линейно деформируемыми. Для них справедлив принцип суперпозиции , в соответствии с которым:
Внутренние усилия, перемещения и деформации от заданной нагрузки (или иного воздействия) можно найти как сумму соответствующих величин от каждой нагрузки в отдельности.
Примечания:
1. Первое из статических уравнений (1.10) получается из условия равновесия рассматриваемого элемента рамы. Полагая в его пределах q x = const, и составляя уравнение X = 0, получим:
– N + q x dx + (N +dN ) = 0,
откуда и следует искомая зависимость. Два других уравнения из (1.10) – это дифференциальные зависимости Журавского .
2. Первое из физических уравнений (1.12) представляет собой дифференциальное уравнение изогнутой оси балки :
κ = d /dx = d 2 v /dx 2 = M /EJ .
Второе уравнение в предпосылке равномерного распределения касательных напряжений в поперечном сечении стержня ( =1) выражает закон Гука при сдвиге :
= Q /F = G .
При этом мы не уточняем смысл коэффициента по причине, которая будет указана в § 3.5. Последнее из физических уравнений (1.12) – это закон Гука при ЦРС :
= N /F = E .
3. В дальнейшем, если не будет оговорено особо, мы будет по-прежнему применять обозначение Oxy для глобальной системы координат, связанной с конструкцией в целом.