Криволинейный интеграл 2-ого рода вычисляется так же, как криволинейный интеграл 1-ого рода сведением к определённому. Для этого все переменные под знаком интеграла выражают через одну переменную, используя уравнение той линии, вдоль которой производится интегрирование.
а) Если линия АВ задана системой уравнений то
 (10.3)
(10.3)
Для плоского случая, когда кривая задана уравнением  криволинейный интеграл вычисляется по формуле: . (10.4)
криволинейный интеграл вычисляется по формуле: . (10.4)
Если линия АВ задана параметрическими уравнениями то
 (10.5)
(10.5)
Для плоского случая, еслилиния АВ
задана параметрическими уравнениями  , криволинейный интеграл вычисляется по формуле:
, криволинейный интеграл вычисляется по формуле:
, (10.6)
где - значения параметра t, соответствующие начальной и конечной точкам пути интегрирования.
Если линия АВ кусочно-гладкая, то следует воспользоваться свойством аддитивности криволинейного интеграла, разбив АВ на гладкие дуги.
Пример 10.1
Вычислим криволинейный интеграл  вдоль контура, состоящего из части кривой
вдоль контура, состоящего из части кривой  от точки
от точки  до
до  и дуги эллипса
и дуги эллипса  от точки
от точки  до
до  .
.
 . Сведём оба интеграла к определённым. Часть контура задана уравнением относительно переменной
. Сведём оба интеграла к определённым. Часть контура задана уравнением относительно переменной  . Воспользуемся формулой (10.4
), в которой поменяем ролями переменные. Т.е.
. Воспользуемся формулой (10.4
), в которой поменяем ролями переменные. Т.е.
 . После вычисления получим
. После вычисления получим  .
.
Для вычисления интеграла по контуру ВС перейдём к параметрической форме записи уравнения эллипса и воспользуемся формулой (10.6).
Обратите внимание на пределы интегрирования. Точке  соответствует значение , а точке
соответствует значение , а точке  соответствует
соответствует  Ответ:
Ответ:  .
.
Пример 10.2. Вычислим вдоль отрезка прямой АВ , где А(1,2,3), В(2,5,8).
Решение
. Задан криволинейный интеграл 2-ого рода. Для вычисления необходимо преобразовать его в определённый. Составим уравнения прямой. Её направляющий вектор имеет координаты  .
.
Канонические уравнения прямой АВ:  .
.
Параметрические уравнения этой прямой:  ,
, 
При  .
.
Воспользуемся формулой (10.5) :
Вычислив интеграл, получим ответ:  .
.
5. Работа силы при перемещении материальной точки единичной массы из точки в точку вдоль кривой .
Пусть в каждой точке кусочно –гладкой кривой  задан вектор, имеющий непрерывные функции-координаты: . Разобьём эту кривую на малых частей точками
задан вектор, имеющий непрерывные функции-координаты: . Разобьём эту кривую на малых частей точками  так, чтобы в точках каждой части
так, чтобы в точках каждой части  значение функций
значение функций  можно было считать постоянными, а сама часть
можно было считать постоянными, а сама часть  могла быть принята за отрезок прямой (см. рис. 10.1). Тогда
могла быть принята за отрезок прямой (см. рис. 10.1). Тогда  . Скалярное произведение постоянной силы, роль которой играет вектор
. Скалярное произведение постоянной силы, роль которой играет вектор  , на прямолинейный вектор перемещения численно равно работе, которую совершает сила при перемещении материальной точки вдоль
, на прямолинейный вектор перемещения численно равно работе, которую совершает сила при перемещении материальной точки вдоль  . Составим интегральную сумму
. Составим интегральную сумму  . В пределе при неограниченном увеличении числа разбиений получим криволинейный интеграл 2-ого рода
. В пределе при неограниченном увеличении числа разбиений получим криволинейный интеграл 2-ого рода
. (10.7)
Таким образом, физический смысл криволинейного интеграла 2-ого рода  - это работа, произведённая силой
- это работа, произведённая силой  при перемещении материальной точки от А
к В
по контуру L
.
при перемещении материальной точки от А
к В
по контуру L
.
Пример 10.3.
Вычислим работу, производимую вектором  при перемещении точки вдоль части кривой Вивиани, заданной как пересечение полусферы
при перемещении точки вдоль части кривой Вивиани, заданной как пересечение полусферы  и цилиндра
и цилиндра 
 , пробегаемой против часовой стрелки, если смотреть с положительной части оси OX.
, пробегаемой против часовой стрелки, если смотреть с положительной части оси OX.
Решение . Построим заданную кривую как линию пересечения двух поверхностей (см. рис. 10.3).
 .
.
Чтобы свести подынтегральное выражение к одной переменной, перейдём в цилиндрическую систему координат:  .
.
Т.к. точка перемещается по кривой  , то удобно в качестве параметра выбрать переменную , которая вдоль контура меняется так, что
, то удобно в качестве параметра выбрать переменную , которая вдоль контура меняется так, что  . Тогда получаем следующие параметрические уравнения этой кривой:
. Тогда получаем следующие параметрические уравнения этой кривой:
 .При этом
.При этом  .
.
Подставим полученные выражения в формулу для вычисления циркуляции:
( - знак + указывает на то, что движение точки по контуру происходит против часовой стрелки)
Вычислим интеграл и получим ответ:  .
.
Занятие 11 .
Формула Грина для односвязной области. Независимость криволинейного интеграла от пути интегрирования. Формула Ньютона-Лейбница. Нахождение функции по ее полному дифференциалу с помощью криволинейного интеграла (плоский и пространственный случаи).
ОЛ-1 гл.5, ОЛ-2 гл.3, ОЛ-4 гл.3 § 10, п. 10.3, 10.4.
Практика : ОЛ-6№№ 2318(а,б,д),2319(а,в),2322(а,г),2327,2329 илиОЛ-5 №№10.79, 82, 133, 135, 139.
Домашнее здание к занятию 11 : ОЛ-6 №№ 2318 (в,г), 2319(в,г), 2322(б,в), 2328, 2330 или ОЛ-5 №№ 10.80, 134, 136, 140
Формула Грина.
Пусть на плоскости  дана односвязная область , ограниченная кусочно- гладким замкнутым контуром . (Область называется односвязной, если в ней любой замкнутый контур может быть стянут в точку этой области).
дана односвязная область , ограниченная кусочно- гладким замкнутым контуром . (Область называется односвязной, если в ней любой замкнутый контур может быть стянут в точку этой области).

Теорема
. Если функции  и их частные производные
и их частные производные  Г
, то
Г
, то
| Рисунок 11.1 |
- формула Грина . (11.1)
Обозначает положительное направление обхода (против часовой стрелки).
Пример 11.1.
Используя формулу Грина, вычислим интеграл  по контуру, состоящему из отрезков OA, OB
и большей дуги окружности
по контуру, состоящему из отрезков OA, OB
и большей дуги окружности  , соединяющей точки A
и B,
если
, соединяющей точки A
и B,
если  ,
,  ,
,  .
.
 Решение
. Построим контур
Решение
. Построим контур  (см. рис.11.2). Вычислим необходимые производные.
(см. рис.11.2). Вычислим необходимые производные.
| Рисунок 11.2 |
 ,
,  ;
;  ,
,  . Функции и их производные непрерывны в замкнутой области, ограниченной данным контуром. По формуле Грина данный интеграл .
. Функции и их производные непрерывны в замкнутой области, ограниченной данным контуром. По формуле Грина данный интеграл .
После подстановки вычисленных производных получаем
 . Двойной интеграл вычислим, переходя к полярным координатам:
. Двойной интеграл вычислим, переходя к полярным координатам:  .
.
Проверим ответ, вычислив интеграл непосредственно по контуру как криволинейный интеграл 2-ого рода.  .
.

Ответ
:  .
.
2. Независимость криволинейного интеграла от пути интегрирования .
Пусть  и
и  - произвольные точки односвязной области пл.
- произвольные точки односвязной области пл.  . Криволинейные интегралы, вычисленные по различным кривым, соединяющим эти точки, в общем случае имеют различные значения. Но при выполнении некоторых условий все эти значения могут оказаться одинаковыми. Тогда интеграл не зависит от формы пути, а зависит только от начальной и конечной точек.
. Криволинейные интегралы, вычисленные по различным кривым, соединяющим эти точки, в общем случае имеют различные значения. Но при выполнении некоторых условий все эти значения могут оказаться одинаковыми. Тогда интеграл не зависит от формы пути, а зависит только от начальной и конечной точек.
Имеют место следующие теоремы.
Теорема 1
. Для того, чтобы интеграл  не зависел от формы пути, соединяющего точки и , необходимо и достаточно, чтобы этот интеграл по любому замкнутому контуру был равен нулю.
не зависел от формы пути, соединяющего точки и , необходимо и достаточно, чтобы этот интеграл по любому замкнутому контуру был равен нулю.
Теорема 2.
. Для того, чтобы интеграл  по любому замкнутому контуру был равен нулю, необходимо и достаточно, чтобы функции
по любому замкнутому контуру был равен нулю, необходимо и достаточно, чтобы функции  и их частные производные
и их частные производные  были непрерывны в замкнутой области Г
и чтобы выполнялось условие
были непрерывны в замкнутой области Г
и чтобы выполнялось условие  (11.2)
(11.2)
Таким образом, если выполняются условия независимости интеграла от формы пути (11.2) , то достаточно указать только начальную и конечную точки: (11.3)
Теорема 3.
Если в односвязной областивыполняется условие  , то существует функция
, то существует функция  такая, что . (11.4)
такая, что . (11.4)
Эта формула называется формулой Ньютона – Лейбница для криволинейного интеграла.
Замечание.
Напомним, что равенство  является необходимым и достаточным условием того, что выражение
является необходимым и достаточным условием того, что выражение 
 .
.
Тогда из выше сформулированных теорем следует, что если функции  и их частные производные
и их частные производные  непрерывны в замкнутой области Г
, в которой даны точки
непрерывны в замкнутой области Г
, в которой даны точки  и
и  , и
, и  , то
, то
а) существует функция  , такая, что ,
, такая, что ,
 не зависит от формы пути, ,
не зависит от формы пути, ,
в) имеет место формула Ньютона – Лейбница .
Пример 11.2
. Убедимся в том, что интеграл  не зависит от формы пути, и вычислим его.
не зависит от формы пути, и вычислим его.
Решение. .
| Рисунок 11.3 |
 Проверим выполнение условия (11.2) .
Проверим выполнение условия (11.2) .  . Как видим, условие выполнено. Значение интеграла не зависит от пути интегрирования. Выберем путь интегрирования. Наиболее
. Как видим, условие выполнено. Значение интеграла не зависит от пути интегрирования. Выберем путь интегрирования. Наиболее
простым путём для вычислений является ломаная линия АСВ , соединяющая точки начала и конца пути. (См. рис. 11.3)
Тогда  .
.

3. Нахождение функции по её полному дифференциалу .
С помощью криволинейного интеграла, который не зависит от формы пути, можно найти функцию  , зная её полный дифференциал. Эта задача решается следующим образом.
, зная её полный дифференциал. Эта задача решается следующим образом.
 Если функции
Если функции  и их частные производные
и их частные производные  непрерывны в замкнутой области Г
и
непрерывны в замкнутой области Г
и  , то выражение является полным дифференциалом некоторой функции
, то выражение является полным дифференциалом некоторой функции  . Кроме этого интеграл
. Кроме этого интеграл  , во-первых, не зависит от формы пути и, во-вторых, может быть вычислен по формуле Ньютона – Лейбница.
, во-первых, не зависит от формы пути и, во-вторых, может быть вычислен по формуле Ньютона – Лейбница.
Вычислим  двумя способами.
двумя способами.
| Рисунок 11.4 |
 с конкретными координатами и точку
с конкретными координатами и точку  с произвольными координатами. Вычислим криволинейный интеграл по ломаной, состоящей из двух отрезков прямых, соединяющих эти точки, причём один из отрезков параллелен оси , а другой – оси . Тогда . (См. рис. 11.4)
с произвольными координатами. Вычислим криволинейный интеграл по ломаной, состоящей из двух отрезков прямых, соединяющих эти точки, причём один из отрезков параллелен оси , а другой – оси . Тогда . (См. рис. 11.4)
Уравнение .
Уравнение .
Получаем: Вычислив оба интеграла, получаем в ответе некоторую функцию  .
.
б) Теперь тот же интеграл вычислим по формуле Ньютона – Лейбница.
Теперь сравним два результата вычисления одного и того же интеграла. Функциональная часть  ответа в пункте а) является искомой функцией
ответа в пункте а) является искомой функцией  , а числовая часть – её значением в точке
, а числовая часть – её значением в точке  .
.
Пример 11.3.
Убедимся в том, что выражение  является полным дифференциалом некоторой функции
является полным дифференциалом некоторой функции  и найдём её. Проверим результаты вычисления примера 11.2 по формуле Ньютона-Лейбница.
и найдём её. Проверим результаты вычисления примера 11.2 по формуле Ньютона-Лейбница.
Решение.
Условие существования функции  (11.2)
было проверено в предыдущем примере. Найдём эту функцию, для чего воспользуемся рисунком 11.4, причём примем за
(11.2)
было проверено в предыдущем примере. Найдём эту функцию, для чего воспользуемся рисунком 11.4, причём примем за  точку
точку  . Составим и вычислим интеграл по ломаной АСВ,
где
. Составим и вычислим интеграл по ломаной АСВ,
где  :
:
Как было сказано выше, функциональная часть полученного выражения и есть искомая функция  .
.
Проверим результат вычислений из примера 11.2 по формуле Ньютона –Лейбница:
Результаты совпали.
Замечание. Все рассмотренные утверждения верны и для пространственного случая, но с большим количеством условий.
Пусть кусочно-гладкая кривая принадлежит области в пространстве  . Тогда, если функции и их частные производные непрерывны в замкнутой области , в которой даны точки
. Тогда, если функции и их частные производные непрерывны в замкнутой области , в которой даны точки  и
и  , и
, и  (11.5
), то
(11.5
), то
а) выражение является полным дифференциалом некоторой функции  ,
,
б) криволинейный интеграл от полного дифференциала некоторой функции  не зависит от формы пути и ,
не зависит от формы пути и ,
в) имеет место формула Ньютона – Лейбница .(11.6 )
Пример 11.4
. Убедимся в том, что выражение является полным дифференциалом некоторой функции  и найдём её.
и найдём её.
Решение.
Для ответа на вопрос о том, является ли данное выражение полным дифференциалом некоторой функции  , вычислим частные производные от функций ,
, вычислим частные производные от функций ,  ,
,  . (См. (11.5)
)
. (См. (11.5)
)  ;
;  ;
;  ;
;  ;
;  ;
;  .
.
Эти функции непрерывны вместе со своими частными производными в любой точке пространства  .
.
Видим, что выполняются необходимые и достаточные условия существования  :
:  ,
,  ,
,  , ч. т. д.
, ч. т. д.
Для вычисления функции  воспользуемся тем, что линейный интеграл не зависит от пути интегрирования и может быть вычислен по формуле Ньютона-Лейбница. Пусть точка
воспользуемся тем, что линейный интеграл не зависит от пути интегрирования и может быть вычислен по формуле Ньютона-Лейбница. Пусть точка  - начало пути, а некоторая точка
- начало пути, а некоторая точка  - конец пути.
Вычислим интеграл
- конец пути.
Вычислим интеграл
 по контуру, состоящему из отрезков прямых, параллельных координатным осям. (см.рис.11.5).
по контуру, состоящему из отрезков прямых, параллельных координатным осям. (см.рис.11.5).
 .
.
| Рисунок 11.5 |
 ,
,  ,
,  .
.
Тогда 
 , x
здесь зафиксирован, поэтому
, x
здесь зафиксирован, поэтому  ,
,
 , здесь зафиксирован y
, поэтому
, здесь зафиксирован y
, поэтому  .
.
В итоге получаем: .
Теперь тот же интеграл вычислим по формуле Ньютона-Лейбница.
Приравняем результаты: .
Из полученного равенства следует, что , а 
Занятие 12.
Поверхностный интеграл первого рода: определение, основные свойства. Правила вычисления поверхностного интеграла первого рода с помощью двойного интеграла. Приложения поверхностного интеграла первого рода: площадь поверхности, масса материальной поверхности, статические моменты относительно координатных плоскостей, моменты инерции и координаты центра тяжести . ОЛ-1 гл.6, ОЛ 2 гл.3, ОЛ-4§ 11.
Практика : ОЛ-6 №№ 2347, 2352, 2353 или ОЛ-5 №№ 10.62, 65, 67.
Домашнее задание к занятию 12:
ОЛ-6 №№ 2348, 2354 или ОЛ-5 №№ 10.63, 64, 68.
Вычисление объема удобнее вести в цилиндрических координатах. Уравнение окружности, ограничивающей областьD , конуса и параболоида
соответственно принимают вид ρ = 2, z = ρ , z = 6 − ρ 2 . С учетом того, что данное тело симметрично относительно плоскостей xOz и yOz . имеем
6− ρ 2 |
||||
V = 4 ∫ 2 dϕ ∫ ρ dρ ∫ dz = 4 ∫ 2 dϕ ∫ ρ z |
6 ρ − ρ 2 d ρ = |
|||
4 ∫ d ϕ∫ (6 ρ − ρ3 − ρ2 ) d ρ =
2 d ϕ = |
|||||||||||||||||
4 ∫ 2 (3 ρ 2 − |
∫ 2 d ϕ = |
32π |
|||||||||||||||
Если не учитывать симметрию, то |
|||||||||||||||||
6− ρ 2 |
32π |
||||||||||||||||
V = ∫ |
dϕ ∫ ρ dρ ∫ dz = |
||||||||||||||||
3. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
Обобщим понятие определенного интеграла на случай, когда областью интегрирования является некоторая кривая. Интегралы такого рода называются криволинейными. Различают два типа криволинейных интегралов: криволинейные интегралы по длине дуги и криволинейные интегралы по координатам.
3.1. Определение криволинейного интеграла первого типа (по длине дуги). Пусть функция f (x, y) определена вдоль плоской кусочно-
гладкой1 кривой L , концами которой будут точки A и B . Разобьем кривую L произвольным образом на n частей точками M 0 = A , M 1 ,... M n = B . На
каждой из частичных дуг M i M i + 1 выберем произвольную точку (x i , y i ) и вычислим значения функции f (x, y) в каждой из этих точек. Сумма
1 Кривая называется гладкой, если в каждой ее точке существует касательная, непрерывно изменяющаяся вдоль кривой. Кусочногладкой кривой называется кривая, состоящая из конечного числа гладких кусков.
n− 1 |
|
σ n = ∑ f (x i , y i ) ∆ l i , |
i = 0
где∆ l i – длина частичной дуги M i M i + 1 , называется интегральной суммой
для функции f (x , y ) по кривой L . Обозначим наибольшую из длин |
|||
частичных дуг M i M i + 1 , i = |
|||
0 ,n − 1 черезλ , то есть λ = max ∆ l i . |
|||
0 ≤i ≤n −1 |
|||
Если существует конечный предел I интегральной суммы (3.1) |
|||
стремлении к нулю наибольшей из длин частичных дугM i M i + 1 , |
|||
зависящий ни от способа разбиения кривой L на частичные дуги, ни от |
|||
выбора точек (x i , y i ) , то этот предел называется криволинейным интегралом первого типа (криволинейным интегралом по длине дуги) от функции f (x , y ) по кривой L и обозначается символом ∫ f (x , y ) dl .
Таким образом, по определению |
||
n− 1 |
||
I = lim ∑ f (xi , yi ) ∆ li = ∫ f (x, y) dl. |
||
λ → 0 i = 0 |
||
Функция f (x , y ) называется в этом случае интегрируемой вдоль кривой L ,
кривая L = AB - контуром интегрирования, А – начальной, а В - конечной точками интегрирования, dl - элементом длины дуги.
Замечание 3.1. Если в (3.2) положить f (x , y ) ≡ 1 для (x , y ) L , то
получим выражение длины дуги L в виде криволинейного интеграла первого типа
l = ∫ dl.
Действительно, из определения криволинейного интеграла следует, |
||||
dl = lim n − 1 |
||||
∆l |
Lim l = l . |
|||
λ → 0 ∑ |
λ→ 0 |
|||
i = 0 |
||||
3.2. Основные свойства криволинейного интеграла первого типа |
||||
аналогичны свойствам определенного интеграла: |
||||
1 о . ∫ [ f1 (x, y) ± f2 (x, y) ] dl = ∫ f1 (x, y) dl ± ∫ f2 (x, y) dl. |
||||
2 о . ∫ cf (x , y ) dl = c ∫ f (x , y ) dl , где с - константа. |
||||
и L , не |
||||
3 о . Если контур интегрирования L разбит на две части L |
||||
имеющие общих внутренних точек, то

∫ f (x, y)dl = ∫ f (x, y)dl + ∫ f (x, y)dl.
4 о .Отметим особо, что величина криволинейного интеграла первого типа не зависит от направления интегрирования, так как в формировании интегральной суммы (3.1) участвуют значения функции f (x , y ) в
произвольных точках и длины частичных дуг ∆ l i , которые положительны,
независимо от того, какую точку кривой AB считать начальной, а какую – конечной, то есть
f (x, y) dl = ∫ f (x, y) dl . |
|||
3.3. Вычисление криволинейного интеграла первого типа |
|||
сводится к вычислению определенных интегралов. |
|||
x= x(t) |
|||
Пусть кривая L задана параметрическими уравнениями |
y= y(t) |
||
Пустьα и β – значения параметра t , соответствующие началу (точка А ) и |
|||||||||||||||||||||||||||||||||
концу (точка В ) |
[α , β ] |
||||||||||||||||||||||||||||||||
x (t ), y (t ) и |
производные |
x (t), y (t) |
Непрерывны, |
f (x , y ) - |
|||||||||||||||||||||||||||||
непрерывна вдоль кривой L . Из курса дифференциального исчисления |
|||||||||||||||||||||||||||||||||
функций одной переменной известно, что |
|||||||||||||||||||||||||||||||||
dl = (x (t)) |
+ (y (t )) |
||||||||||||||||||||||||||||||||
∫ f (x, y) dl = ∫ f (x(t), y(t)) |
|||||||||||||||||||||||||||||||||
(x (t ) |
+ (y (t )) |
||||||||||||||||||||||||||||||||
∫ x2 dl, |
|||||||||||||||||||||||||||||||||
Пример 3.1. |
Вычислить |
окружности |
|||||||||||||||||||||||||||||||
x= a cos t |
|||||||||||||||||||||||||||||||||
0 ≤ t ≤ |
|||||||||||||||||||||||||||||||||
y= a sin t |
|||||||||||||||||||||||||||||||||
Решение. Так как x (t ) = − a sin t , y (t ) = a cos t , то |
|||||||||||||||||||||||||||||||||
dl = |
(− a sin t) 2 + (a cos t) 2 dt = a2 sin 2 t + cos 2 tdt = adt |
||||||||||||||||||||||||||||||||
и по формуле (3.4) получаем |
|||||||||||||||||||||||||||||||||
Cos 2t )dt = |
sin 2t |
||||||||||||||||||||||||||||||||
∫ x2 dl = ∫ a2 cos 2 t adt = a |
3 ∫ |
||||||||||||||||||||||||||||||||
πa 3 |
|||||||||||||||||||||||||||||||||
sin π |
|||||||||||||||||||||||||||||||||

L задана |
уравнением |
y = y(x) , |
a ≤ x ≤ b |
y(x) |
||||||||||||||||
непрерывна вместе со своей производной y |
(x ) при a ≤ x ≤ b , то |
|||||||||||||||||||
dl = |
||||||||||||||||||||
1+ (y (x )) |
||||||||||||||||||||
и формула (3.4) принимает вид |
||||||||||||||||||||
∫ f (x, y) dl = ∫ f (x, y(x)) |
||||||||||||||||||||
(y (x )) |
||||||||||||||||||||
L задана |
x = x(y), c ≤ y ≤ d |
x (y ) |
||||||||||||||||||
уравнением |
||||||||||||||||||||
непрерывна вместе со своей производной x (y ) при c ≤ y ≤ d , то |
||||||||||||||||||||
dl = |
||||||||||||||||||||
1+ (x (y )) |
||||||||||||||||||||
и формула (3.4) принимает вид |
||||||||||||||||||||
∫ f (x, y) dl = ∫ f (x(y), y) |
||||||||||||||||||||
1 + (x (y )) |
||||||||||||||||||||
Пример 3.2. Вычислить ∫ ydl, где L – дуга параболы |
2 x от |
|||||||||||||||||||
точки А (0,0) до точки В (2,2). |
||||||||||||||||||||
Решение . Вычислим интеграл двумя способами, применяя |
||||||||||||||||||||
формулы (3.5) и(3.6) |
||||||||||||||||||||
1)Воспользуемся формулой (3.5). Так как |
||||||||||||||||||||
2x (y ≥ 0), y ′ |
||||||||||||||||||||
2 x = |
2 x , |
dl = |
1+ 2 x dx , |
|||||||||||||||||
3 / 2 2 |
||||||||||||||||||||
1 (5 |
3 2 − 1) . |
|||||||||||||||||||
∫ ydl = ∫ |
2 x + 1 dx = ∫ (2 x + 1) 1/ 2 dx = |
1 (2x + 1) |
||||||||||||||||||
2)Воспользуемся формулой (3.6). Так как |
||||||||||||||||||||
x = 2 , x |
Y, dl |
1 + y |
||||||||||||||||||
y 1 + y 2 dy = |
(1 + y |
/ 2 2 |
||||||
∫ ydl = ∫ |
||||||||
3 / 2 |
||||||||
1 3 (5 5 − 1).
Замечание 3.2. Аналогично рассмотренному, можно ввести понятие криволинейного интеграла первого типа от функции f (x , y , z ) по
пространственной кусочно-гладкой кривой L :

Если кривая L задана параметрическими уравнениями
α ≤ t ≤ β , то
dl = |
||||||||||||||||
(x (t )) |
(y (t )) |
(z (t )) |
||||||||||||||
∫ f (x, y, z) dl = |
||||||||||||||||
= ∫ |
dt . |
|||||||||||||||
f (x (t ), y (t ), z (t )) (x (t )) |
(y (t )) |
(z (t )) |
||||||||||||||
x= x(t) , y= y(t)
z= z(t)
Пример 3.3. Вычислить∫ (2 z − x 2 + y 2 ) dl , где L – дуга кривой
x= t cos t |
0 ≤ t ≤ 2 π. |
|
y = t sin t |
||
z = t |
||
x′ = cost − t sint, y′ = sint + t cost, z′ = 1 , |
||
dl = |
(cos t − t sin t)2 + (sin t + t cos t)2 + 1 dt = |
|
Cos2 t − 2 t sin t cos t + t2 sin2 t + sin2 t + 2 t sin t cos t + t2 cos2 t + 1 dt =
2 + t2 dt .
Теперь по формуле (3.7) имеем
∫ (2z − |
x2 + y2 ) dl = ∫ (2 t − |
t 2 cos 2 t + t 2 sin 2 t ) |
2 + t 2 dt = |
|||||||||||||||||||
T 2 ) |
||||||||||||||||||||||
= ∫ |
t 2 + t |
dt = |
4 π |
− 2 2 |
||||||||||||||||||
цилиндрической |
поверхности, |
|||||||||||||||||||||
которая составлена из перпендикуляров к |
||||||||||||||||||||||
плоскости xOy , |
восстановленных в точках |
|||||||||||||||||||||
(x , y ) |
L = AB |
и имеющих |
||||||||||||||||||||
представляет собой массу кривой L , имеющей переменную линейную плотность ρ (x , y )
линейная плотность которой меняется по закону ρ (x , y ) = 2 y .
Решение. Для вычисления массы дуги AB воспользуемся формулой (3.8). Дуга AB задана параметрически, поэтому для вычисления интеграла (3.8) применяем формулу (3.4). Так как
1+ t |
dt , |
|||||||||||||
x (t) = 1, y (t) = t , dl = |
||||||||||||||
3/ 2 1 |
||||||||||||||
1 (1+ t |
||||||||||||||
m = ∫ 2 ydl = ∫ |
1 2 + t2 dt = ∫ t 1 + t2 dt = |
|||||||||||||
(2 3 / 2 − |
1) = |
2 2 − 1. |
||||||||||||
3.4. Определение криволинейного интеграла второго типа (по |
||||||||||||||
координатам ). Пусть функция |
f (x , y ) определена вдоль плоской |
|||||||||||||
кусочно-гладкой кривойL , концами которой будут точки А и В . Опять |
||||||||||||||
произвольным |
разобьем |
кривую L |
||||||||||||
M 0 = A , M 1 ,... M n = B Так же выберем в пределах |
каждой частичной |
|||||||||||||
дуги M i M i + 1 |
произвольную точку |
(xi , yi ) |
и вычислим |
Кривая АВ, заданная параметрическими уравнениями называется гладкой, если функции и имеют на отрезке непрерывные производные и причем Если в конечном числе точек отрезка эти производные не существуют или одновременно обращаются в нуль, то кривая называете я кусочно-гладкой. Пусть АВ - плоская кривая, гладкая или ку-сочно-гладкая. Пусть f(M) - функция, заданная на кривой АВ или в некоторой области D, содержащей эту кривую. Рассмотрим разбиение кривой А В на части точками (рис. 1). Выберем на каждой из дуг A^At+i произвольную точку Mk и составим сумму где Alt - длина дуги и назовем ее интегральной суммой для функции f(M) по длине дуги кривой. Пусть Д / - наибольшая издлин частичных дуг, т. е. Свойства криволинейных интегралов 1-го рода для пространственных кривых Криволинейные интегралы 2-го рода Вычисление криволинейного интеграла Свойства Связь между Определе нив. Если при интегральная сумма (I) имеет конечный предел, не зависящий ни от способа разбиения кривой АВ на части, ни от выбора точек на каждой из дуг разбиения, то этот предел называется криволинейным интегралом \ -го рода от функции f(M) по кривой АВ (интеграл по длине дуги кривой) и обозначается символом В этом случае функция /(М) называется интегрируемой вдоль кривой АВУ кривая А В называется контуром интегрирования, А - начальной, В - конечной точками интегрирования. Таким образом, по определению, Пример 1. Пусть вдоль некоторой гладкой кривой L распределена масса с переменной линейной плотностью J(M). Найти массу т кривой L. (2) Разобьем кривую L на п произвольных частей) и вычислим приближен- но массу каждой части, предполагая, что на каждой из частей плотность постоянна и равна плотности в какой-нибудь из ее точек, например, в крайней левой точке /(Af*). Тогда сумма кшо где Д/д - длина Дг-ой части, будет приближенным значением массы т. Ясно, что погрешность будет тем меньше, чем мельче разбиение кривой L. В пределе при Ы -* 0 (Д / = max Л/») получим точное значение массы всей кривой L, т.е. Но предел справа есть криволинейный интеграл 1-го рода. Значит, 1.1. Существование криволинейного интеграла 1-го рода Примем на кривой АВ за параметр длину дуги I, отсчитываемую от начальной точки А (рис.2). Тогда кривую АВ можно описать уравнениями (3) где L - длина кривой АВ. Уравнения (3) называются натуральными уравнениями кривой АВ. При переходе к натуральным уравнениям функция f(x} у), заданная на кривой АВ, сведется к функции переменной I: / (х(1)} у(1)). Обозначив через значение параметра I, отвечающее точке Мку перепишем интегральную сумму (I) в виде Это - интегральная сумма, отвечающая определенному интегралу Поскольку интегральные суммы (1) и (4) равны междусобой, то равны и отвечающие им интегралы. Таким образом, (5) Теорема 1. Если функция /(М) непрерывна вдоль гладкой кривой АВ, то существует криволинейный интеграл (поскольку при этих условиях существует определенный интеграл, стоящий в равенстве (5) справа). 1.2. Свойства криволинейных интегралов 1-го рода 1. Из вида интегральной суммы (1) следует, что т.е. величина криволинейного интеграла 1-го рода не зависит ог направления интегрирования. 2. Линейность. Если для каждой из функций /() существует криволинейный интеграл по кривой ABt то для функции а/, где а и /3 - любые постоянные, также существует криволинейный интеграл по кривой АВ> причем 3. Аддитивность. Если кривая АВ состоит из двух кусков и для функции /(М) существует криволинейный интеграл по АВУ то существуют интегралы причем 4. Если 0 на кривой АВ, то 5. Если функция интегрируема на кривой АВ, то функция || также интегрируема на А В, и при этом б. Формула среднего значения. Если функция / непрерывна вдоль кривой АВ, то на этой кривой найдется точка Мс такая, что где L - длина кривой АВ. 1.3. Вычисление криволинейного интеграла 1-го рода Пусть кривая АВ задана параметрическими уравнениями причем точке А соответствует значение t = to, а точке В - значение. Будем предполагать, что функции) непрерывны на вместе со своими производными и выполнено неравенство Тогда дифференциал дуги кривой вычисляется по формуле В частности, если кривая АВ задана явным уравнением непрерывно дифференцируема на [а, Ь] и точке А соответствует значение х = а, а точке В - значение х = 6, то, принимая х за параметр, получаем 1.4. Криволинейные интегралы 1-го рода для пространственных кривых Определение криволинейного интеграла 1-го рода, сформулированное выше для плоской кривой, дословно переносится на случай, когда функция f(M) задана вдоль некоторой пространственной кривой АВ. Пусть кривая АВ задана параметрическими уравнениями Свойства криволинейных интегралов 1-го рода для пространственных кривых Криволинейные интегралы 2-го рода Вычисление криволинейного интеграла Свойства Связь между Тогда криволинейный интеграл взятый вдоль этой кривой, можно свести к определенному интегралу при помоши следующей формулы: Пример 2. Вычислитькриволинейный интеграл где L - контур треугольнике с вершинами в точка* (рис.3). По свойству аддитивности имеем Вычислим каждый из интегралов в отдельности. Так как на отрезке OA имеем: , то На отрезке АН имеем, откуда причем тогда Рис. Наконец, Следовательно, Замечание. При вычислении интегралов мы воспользовались свойством 1, согласно которому. Криволинейные интегралы 2-го рода Пусть А В - гладкая или кусочно-гладкая ориентированная кривая на плоскости хОу и пусть - вектор-функция, определенная в некоторой области D, содержащей кривую АВ. Разобьем кривую АВ на части точками координаты которых обозначим соответственно через (рис. 4). На каждой из элементарныхдуг АкАк+\ возьмем произвольно точку и составим сумму Пусть Д/ - длина наибольшей из дуг Определение. Если при сумма (1) имеет конечный предел, не зависящий ни от способа разбиения кривой АВ, ни от выбора точек rjk) на элементарных дугах, то этот предел называется криволинейным интегралом 2-города от вектор-функции по кривой АВ и обозначается символом Так что по определению Теорема 2. Если в некоторой области D, содержащей кривую АВ, функции непрерывны, то криволинейный интеграл 2-города существует. Пусть - радиус-вектор точки М(х, у). Тогда и подынтегральное выражение в формуле (2) можно представить в виде скалярного произведения векторов F(M) и dr. Так что интеграл 2-го рода от вектор-функции по кривой АВ можно записать коротко так: 2.1. Вычисление криволинейного интеграла 2-го рода Пусть кривая АВ задана параметрическими уравнениями, где функции непрерывны вместе с производными на отрезке, причем изменению параметра t от t0 до t\ соответствует движение точки по кривой АВ отточки А к точке В. Если в некоторой области D, содержащей кривую АВ, функции непрерывны, то криволинейный интеграл 2-го рода сводится к следующему определенному интегралу: Таким образом, вычисление криволинейного интеграла 2-го рода также может быть сведено к вычислению определенного интеграла. О) Пример 1. Вычислить интеграл вдоль прямолинейного отрезка, соединяющего точки 2) вдоль параболы, соединяющей те же тонки) Уравнение линии параметр, откуда Так что 2) Уравнение линии AB: Отсюда поэтому Рассмотренный пример помазывает, что величина криволинейного интеграла 2-го рода, вообще говоря, зависитот формы пути интегрирования. 2.2. Свойства криволинейного интеграл а 2-го рода 1. Линейность. Если существуют Свойства криволинейных интегралов 1-го рода для пространственных кривых Криволинейные интегралы 2-го рода Вычисление криволинейного интеграла Свойства Связь между то при любых действительных а и /5 существует и интеграл причем 2. Аддитеностъ. Если кривая АВ разбита на части АС и СБ и криволинейный интеграл существует, то существуют и нтегралы Последнее свойство соитвггггнусг физической интерпретации криволинейного интеграла 2-го рода ках работы силового поля F вдоль некоторого путь: при изменении направления дешкения по кривой работа силового поля вдоль этой кривой меняет знак на противоположный. 2.3. Связь между криволинейными интегралами 1-го и 2-го рода Рассмотрим криволинейный интеграл 2-го рода где ориентированная кривая АВ (А - начальная точка, В - конечная точка) задана векгорным уравнением (здесь I - длина кривой, отсчитываемая в том направлении, в котором ориентирована кривая АВ) (рис. 6). Тогда dr или где г = т(1) - единичный вектор касательной к кривой АВ в точке М(1). Тогда Заметим, что последний интеграл в этой формуле - криволинейный интеграл 1-го рода. При изменении ориентации кривой АВ единичный вектор касательной г заменяется на противоположный вектор (-г), что влечет изменение знака его подынтегрального выражения и, значит, знака самого интеграла. Кафедра «Высшая математика» Криволинейные интегралы Методические указания Волгоград УДК 517.373(075) Рецензент: старший преподаватель кафедры «Прикладная математика» Н.И. Кольцова Печатается по решению редакционно-издательского совета Волгоградского государственного технического университета Криволинейные интегралы: метод. указания / сост. М.И.Андреева, О.Е. Григорьева; ВолгГТУ. – Волгоград, 2011. – 26 с. Методические указания являются руководством к выполнению индивидуальных заданий по теме « Криволинейные интегралы и их приложения к теории поля». В первой части методических указаний содержится необходимый теоретический материал для выполнения индивидуальных заданий. Во второй части рассмотрены примеры выполнения всех типов заданий, включенных в индивидуальные задания по теме, что способствует лучшей организации самостоятельной работы студентов и успешному усвоению темы. Методические указания предназначены для студентов первого и второго курсов. © Волгоградский государственный технический университет, 2011
Определение криволинейного интеграла 1 рода Пусть È АВ – дуга плоской или пространственной кусочно-гладкой кривой L , f (P ) – заданная на этой дуге непрерывная функция, А 0 = А , А 1 , А 2 , …, А n – 1 , А n = B АВ и P i – произвольные точки на частичных дугах È А i – 1 A i , длины которых Dl i (i = 1, 2, …, n
при n ® ¥ и max Dl i ® 0, который не зависит ни от способа разбиения дуги È АВ точками A i , ни от выбора точек P i на частичных дугах È А i – 1 A i (i = 1, 2, …, n ). Этот предел называется криволинейным интегралом 1 рода от функции f (P ) по кривой L и обозначается Вычисление криволинейного интеграла 1 рода Вычисление криволинейного интеграла 1 рода может быть сведено к вычислению определенного интеграла при разных способах задания кривой интегрирования.
Если дуга È АВ плоской кривой задана параметрически уравнениями где x (t ) и y (t t , причем x (t 1) = x A , x (t 2) = x B , то где Аналогичная формула имеет место в случае параметрического задания пространственной кривой L . Если дуга ÈАВ кривой L задана уравнениями , и x (t ), y (t ), z (t ) – непрерывно дифференцируемые функции параметра t , то где - дифференциал длины дуги кривой.
в декартовых координатах Если дуга ÈАВ
плоской кривой L
задана уравнением
и формула для вычисления криволинейного интеграла имеет вид: При задании дуги ÈАВ
плоской кривой L
в виде x
= x
(y
), y
Î [y
1 ; y
2 ],
и криволинейный интеграл вычисляется по формуле
Задание кривой интегрирования полярным уравнением Если плоская кривая L задана уравнением в полярной системе координат r = r (j), j Î , где r (j) – непрерывно дифференцируемая функция, то
Приложения криволинейного интеграла 1 рода С помощью криволинейного интеграла 1 рода вычисляются: длина дуги кривой, площадь части цилиндрической поверхности, масса, статические моменты, моменты инерции и координаты центра тяжести материальной кривой с заданной линейной плотностью. 1. Длина l плоской или пространственной кривой L находится по формуле 2. Площадь части цилиндрической поверхности с параллельной оси OZ образующей и расположенной в плоскости XOY направляющей L , заключенной между плоскостью XOY и поверхностью, задаваемой уравнением z = f (x ; y ) (f (P ) ³ 0 при P Î L ), равна
3. Масса m материальной кривой L с линейной плотностью m(P ) определяется формулой
4. Статические моменты относительно осей Ox и Oy и координаты центра тяжести плоской материальной кривой L с линейной плотностью m(x ; y ) соответственно равны:
5. Статические моменты относительно плоскостей Oxy , Oxz , Oyz и координаты центра тяжести пространственной материальной кривой с линейной плотностью m(x ; y ; z) определяются по формулам:
6. Для плоской материальной кривой L с линейной плотностью m(x ; y ) моменты инерции относительно осей Ox , Oy и начала координат соответственно равны:
7. Моменты инерции пространственной материальной кривой L с линейной плотностью m(x ; y ; z) относительно координатных плоскостей вычисляются по формулам
а моменты инерции относительно координатных осей равны:
2. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ 2 РОДА Определение криволинейного интеграла 2 рода Пусть ÈАВ – дуга кусочно-гладкой ориентированной кривой L , = (a x (P ); a y (P ); a z (P )) – заданная на этой дуге непрерывная векторная функция, А 0 = А , А 1 , А 2 , …, А n – 1 , А n = B – произвольное разбиение дуги АВ и P i – произвольные точки на частичных дугах А i – 1 A i . Пусть – вектор с координатами Dx i , Dy i , Dz i (i = 1, 2, …, n ), и – скалярное произведение векторов и (i = 1, 2, …, n ). Тогда существует предел последовательности интегральных сумм
при n
® ¥ и max ÷ ç ® 0, который не зависит ни от способа разбиения дуги АВ
точками A i
, ни от выбора точек P i
на частичных дугах ÈА i
– 1 A i
В случае, когда векторная функция задана на плоской кривой L , аналогично имеем: При изменении направления интегрирования криволинейный интеграл 2 рода меняет знак. Криволинейные интегралы первого и второго рода связаны соотношением
где – единичный вектор касательной к ориентированной кривой. С помощью криволинейного интеграла 2 рода можно вычислять работу силы при перемещении материальной точки по дуге кривой L:
Положительным направлением обхода замкнутой кривой С, ограничивающей односвязную область G , считается обход против часовой стрелки. Криволинейный интеграл 2 рода по замкнутой кривой С называется циркуляцией и обозначается
Вычисление криволинейного интеграла 2 рода Вычисление криволинейного интеграла 2 рода сводится к вычислению определенного интеграла. Параметрическое задание кривой интегрирования Если ÈАВ ориентированной плоской кривой задана параметрически уравнениями , где х (t ) и y (t ) – непрерывно дифференцируемые функции параметра t , причем то
Аналогичная формула имеет место в случае параметрического задания пространственной ориентированной кривой L
. Если дуга ÈАВ
кривой L
задана уравнениями , и
Явное задание плоской кривой интегрирования Если дуга ÈАВ L задана в декартовых координатах уравнением где y (x ) – непрерывно дифференцируемая функция, то
При задании дуги ÈАВ
плоской ориентированной кривой L
в виде
Пусть функции
в плоской замкнутой области G , ограниченной кусочно-гладкой замкнутой самонепересекающейся положительно ориентированной кривой С + . Тогда имеет место формула Грина: Пусть G – поверхностно-односвязная область, и = (a x (P ); a y (P ); a z (P )) – заданное в этой области векторное поле. Поле (P ) называется потенциальным, если существует такая функция U (P ), что (P ) = grad U (P ), Необходимое и достаточное условие потенциальности векторного поля (P ) имеет вид: rot (P ) = , где (2.10)
Если векторное поле является потенциальным, то криволинейный интеграл 2 рода не зависит от кривой интегрирования, а зависит только от координат начала и конца дуги М 0 М . Потенциал U (М ) векторного поля определяется с точностью до постоянного слагаемого и находится по формуле
где М 0 М – произвольная кривая, соединяющая фиксированную точку М 0 и переменную точку М . Для упрощения вычислений в качестве пути интегрирования может быть выбрана ломаная М 0 М 1 М 2 М со звеньями, параллельными координатным осям, например:
3. примеры выполнения заданий Задание 1 Вычислить криволинейный интеграл I рода где L – дуга кривой , 0 ≤ x ≤ 1. Решение. По формуле (1.3) сведения криволинейного интеграла I рода к определенному интегралу в случае гладкой плоской явно заданной кривой:
где y
= y
(x
), x
0 ≤ x
≤ x
1 – уравнение дуги L
кривой интегрирования. В рассматриваемом примере
и дифференциал длины дуги кривой L
то, подставляя в это выражение Преобразуем криволинейный интеграл к определенному: Вычисляем этот интеграл с помощью подстановки . Тогда
Задание 2 Вычислить криволинейный интеграл 1 рода Решение. Так как L – дуга гладкой плоской кривой, заданной в параметрическом виде, то используем формулу (1.1) сведения криволинейного интеграла 1 рода к определенному:
В рассматриваемом примере Найдем дифференциал длины дуги
Найденные выражения подставляем в формулу (1.1) и вычисляем:
Задание 3 Найти массу дуги линии L с линейной плоскостью m. Решение. Масса m дуги L с плотностью m(P ) вычисляется по формуле (1.8)
Это криволинейный интеграл 1 рода по параметрически заданной гладкой дуге кривой в пространстве, поэтому он вычисляется по формуле (1.2) сведения криволинейного интеграла 1 рода к определенному интегралу: Найдем производные и дифференциал длины дуги
Задание 4 Пример 1. Вычислить криволинейный интеграл 2 рода
по дуге L кривой 4x + y 2 = 4 от точки A (1; 0) до точки B (0; 2). Решение. Плоская дуга L задана в неявном виде. Для вычисления интеграла удобнее выразить x через y : и находить интеграл по формуле (2.8) преобразования криволинейного интеграла 2 рода в определенный интеграл по переменной y : где a x (x ; y ) = xy – 1, a y (x ; y ) = xy 2 . С учетом задания кривой
По формуле (2.8) получаем
Пример 2 . Вычислить криволинейный интеграл 2 рода
где L – ломаная ABC , A (1; 2), B (3; 2), C (2; 1). Решение . По свойству аддитивности криволинейного интеграла Каждый из интегралов- слагаемых вычисляем по формуле (2.7)
где a x (x ; y ) = x 2 + y , a y (x ; y ) = –3xy .
Уравнение отрезка прямой AB : y = 2, y ¢ = 0, x 1 = 1, x 2 = 3. Подставляя в формулу (2.7) эти выражения, получаем:
Для вычисления интеграла
составим уравнение прямой BC по формуле
где x B , y B , x C , y C – координаты точек B и С . Получаем
Подставляем полученные выражения в формулу (2.7):
Задание 5 Вычислить криволинейный интеграл 2 рода по дуге L
Решение . Так как кривая интегрирования задана параметрически уравнениями x = x (t ), y = y (t ), t Î [t 1 ; t 2 ], где x (t ) и y (t ) – непрерывно дифференцируемые функции t при t Î [t 1 ; t 2 ], то для вычисления криволинейного интеграла второго рода используем формулу (2.5) сведения криволинейного интеграла к определенному для плоской параметрически заданной кривой В рассматриваемом примере a x (x ; y ) = y ; a y (x ; y ) = –2x . C учетом задания кривой L получаем:
Подставляем найденные выражения в формулу (2.5) и вычисляем определенный интеграл:
Задание 6 Пример 1.
C
+ Решение. Обозначение C + указывает, что обход контура осуществляется в положительном направлении, то есть против часовой стрелки. Проверим, что для решения задачи можно использовать формулу Грина (2.9) Так как функции a x
(x
; y
) = 2y
– x
2 ; a y
(x
; y
) = 3x
+ y
и их частные производные Для вычисления двойного интеграла изобразим область G
, предварительно определив точки пересечения дуг кривых y
2 = 2x
и Точки пересечения найдем, решив систему уравнений:
Второе уравнение системы равносильно уравнению x 2 – 10x + 16 = 0, откуда x 1 = 2, x 2 = 8, y 1 = –2, y 2 = 4. Итак, точки пересечения кривых: A (2; –2), B (8; 4).
Так как область G – правильная в направлении оси Ox , то для сведения двойного интеграла к повторному спроектируем область G на ось OY и воспользуемся формулой
Так как a = –2, b = 4, x 2 (y ) = 4+y , то
Пример 2.
Вычислить криволинейный интеграл 2 рода по замкнутому контуру Решение. Обозначение означает, что контур треугольника обходится по часовой стрелке. В случае, когда криволинейный интеграл берется по замкнутому контуру , формула Грина принимает вид Изобразим область G , ограниченную заданным контуром.
Функции Область G не является правильной в направлении какой-либо из осей. Проведем отрезок прямой x = 1 и представим G в виде G = G 1 È G 2 , где G 1 и G 2 области, правильные в направлении оси Oy . Тогда Для сведения каждого из двойных интегралов по G 1 и G 2 к повторному будем использовать формулу
где [a ; b ] – проекция области D на ось Ox , y = y 1 (x ) – уравнение нижней ограничивающей кривой, y = y 2 (x ) – уравнение верхней ограничивающей кривой. Запишем уравнения границ области G 1 и найдем AB : y = 2x , 0 ≤ x ≤ 1; AD : , 0 ≤ x ≤ 1. Составим уравнение границы BC области G 2 , используя формулу
BC : где 1 ≤ x ≤ 3. DC : 1 ≤ x ≤ 3.
Задание 7 Пример 1.
Найти работу силы Решение
. Работу переменной силы при перемещении материальной точки по дуге кривой L
определяем по формуле (2.3) (как криволинейный интеграл второго рода от функции по кривой L
) Так как векторная функция задана уравнением и дуга плоской ориентированной кривой определена явно уравнением y = y (x ), x Î [x 1 ; x 2 ], где y (x ) непрерывно дифференцируемая функция, то по формуле (2.7) В рассматриваемом примере y = x 3 , , x 1 = x M = 0, x 2 = x N = 1. Поэтому
Пример 2
. Найти работу силы Решение . Используя формулу (2.3), получаем
В рассматриваемом примере дуга кривой L (ÈMN ) – это четверть окружности, задаваемой каноническим уравнением x 2 + y 2 = 4. Для вычисления криволинейного интеграла второго рода удобнее перейти к параметрическому заданию окружности: x = R cost , y = R sint и воспользоваться формулой (2.5) Так как x
= 2cost
, y
= 2sint
,
Задание 8 Пример 1
. Вычислить модуль циркуляции векторного поля Решение. Для вычисления циркуляции векторного поля вдоль замкнутого контура Г воспользуемся формулой (2.4)
Так как задано пространственное векторное поле Кривая Г задана как пересечение двух поверхностей: гиперболического параболоида z = x 2 – y 2 + 2 и цилиндра x 2 + y 2 = 1. Для вычисления криволинейного интеграла удобно перейти к параметрическим уравнениям кривой Г . Уравнение цилиндрической поверхности можно записать в виде: Так как входящие в параметрические уравнения кривой Г
функции
Самое обсуждаемое
 | ||||||||||

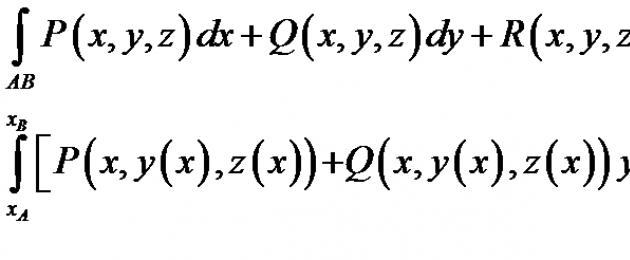
 .
.
 .
.
 .
. .
.

 (1.4)
(1.4) (1.5)
(1.5)
 (2.5)
(2.5) (2.6)
(2.6) (2.7)
(2.7) (2.8)
(2.8)
 (2.11)
(2.11)


 Находим производную этой функции
Находим производную этой функции
 ,
,
 .
.

 Подставляем эти выражения в формулу для массы:
Подставляем эти выражения в формулу для массы:







 0 ≤ t
≤ 1.
0 ≤ t
≤ 1.

 непрерывны в плоской замкнутой области G
, ограниченной контуром C
, тоформула Грина применима.
непрерывны в плоской замкнутой области G
, ограниченной контуром C
, тоформула Грина применима.

 .
.

 и
и  непрерывны в области G
, поэтому можно применить формулу Грина. Тогда
непрерывны в области G
, поэтому можно применить формулу Грина. Тогда